
Conţinut
- Determinați timpul în aer.
- Pasul 1
- Pasul 2
- Pasul 3
- Pasul 4
- Determinați înălțimea maximă
- Pasul 1
- Pasul 2
- Pasul 3
- Determinați distanța orizontală parcursă.
- Pasul 1
- Pasul 2
- Pasul 3
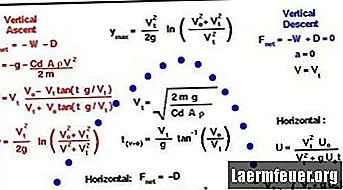
Iată metoda de calcul a traiectoriei unui glonț și, mai exact, a timpului în aer, a razei de acțiune și a celui mai înalt punct al traiectoriei sale. În acest exemplu, s-au făcut câteva presupuneri pentru a simplifica calculul: rezistența neglijabilă a aerului, lipsa vântului și distanța de tragere insuficientă pentru ca rotația Pământului să aibă efect.
Determinați timpul în aer.
Pasul 1
În primul rând, trebuie determinată forma arcului. Dacă unghiul este inițial în jos, atunci cel mai înalt punct este deja cunoscut ca fiind poziția de tragere. Chiar și un unghi ascendent poate avea ținta drept cel mai înalt punct, indiferent dacă acest unghi este superficial sau cu o înălțime suficientă (h). Acest lucru poate fi determinat în pasul patru, când se determină timpul de aer.
Pasul 2
Dacă unghiul „?” rata de tragere este cea dintre traiectoria inițială a proiectilului și orizontală, deci viteza verticală inițială este V (i) = V.sen?.
Pasul 3
Timpul de aer se găsește folosind ecuația poziției h = V.sen? .T - (0,5) g.t ^ 2, unde g = 9,8 metri / secunde ^ 2. Toate variabilele sunt cunoscute, cu excepția timpului în aer, t, deci acest lucru poate fi rezolvat folosind funcția pătratică: ax ^ 2 + bx + c = 0, prin urmare, x = [-b ± √ (b ^ 2-4ac )] / 2a
Pasul 4
Dacă sunt permise mai multe soluții pentru t, deoarece h> 0, atunci primul rezultat corespunde când înălțimea = h pe traseul de ascensiune și al doilea cu când înălțimea = h pe drumul de coborâre. Dacă h <0, atunci singura soluție reală pentru t a fost permisă, iar cealaltă este negativă.
Determinați înălțimea maximă
Pasul 1
Dacă? <0, atunci se știe deja că înălțimea maximă este înălțimea inițială, h = 0.
Pasul 2
Dacă a existat mai mult de o dată, t, în care glonțul se extinde h, atunci cel mai mic t corespunde unei căi de zbor unde h este punctul cel mai înalt. Cel mai mare t corespunde glonțului care atinge o înălțime mai mare înainte de a reveni la h, pentru a rezolva această înălțime, utilizați formula V (t) = V (0) - 9.8t pentru a găsi valoarea lui t când viteza verticală este zero. Cu alte cuvinte, pentru ce oră, t, V.sen? = 9.8t.?
Pasul 3
Rezolvând t și conectând formula înălțimii, avem înălțimea maximă: hm = V.sen? - 4.9t ^ 2. Aceeași abordare este utilizată pentru soluția cu înălțime maximă, dacă a fost permisă o singură soluție pentru t.
Determinați distanța orizontală parcursă.
Pasul 1
Pentru a determina distanța orizontală parcursă până când glonțul atinge înălțimea h, calculați mai întâi viteza orizontală inițială a glonțului: v (i) = V.cos (?).
Pasul 2
Înlocuiți timpul, t, când glonțul atinge înălțimea finală, A, în poziția formulei folosind viteza orizontală: A = V.cosΘ.t. Presupunând că nu există rezistență la aer și nici un termen de accelerare pe partea dreaptă.
Pasul 3
Dacă a existat mai mult de o dată t când înălțimea a fost în h, atunci cele două poziții ale „A” vor fi valabile, punctul cel mai înalt atins fiind hm pentru cea mai mică dintre cele două „A”. Pozițiile finale orizontale și verticale și cel mai înalt punct atins sunt acum cunoscute, determinând astfel traiectoria glonțului.