Conţinut
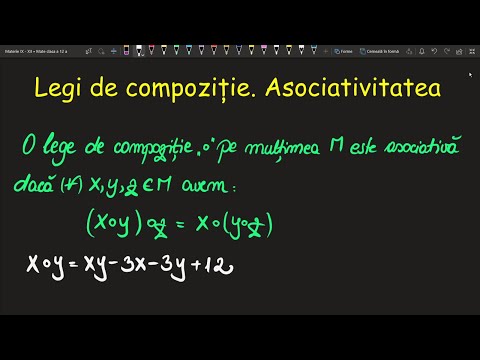
Proprietățile comutative și asociative afectează adăugarea și multiplicarea. Activitățile pentru elevii de clasa a treia care predau aceste proprietăți pot fi făcute utilizând materialele educaționale disponibile sau permițând studenților să fie jucăriile educaționale. Atunci când desfășoară fiecare activitate, provocați elevii să dea sugestii diferite cu privire la modul de obținere a aceluiași rezultat.
Adunarea cu studenții
Împărțiți elevii în grupuri în funcție de gen. Cereți fetelor să numere câte fete are grupul și să înregistreze numărul respectiv. Cereți băieților să numere câte băieți are grupul și înregistrați numărul respectiv. Adăugați numărul de băieți cu fete pentru a obține totalul. Afișați apoi cum adăugarea numărului de băieți la numărul de fete, schimbând ordinea în funcție de proprietatea comutativă, dă același rezultat.
Extinderea grupului de elevi
Împărțiți elevii în trei grupuri. Alegeți un criteriu aleatoriu: puteți alege copii care poartă aceeași culoare sau alegeți după data nașterii, de exemplu. Cereți copiilor să numere numărul de membri ai grupului. Adăugați numărul de grupuri în diferite moduri pentru a demonstra proprietatea comutativă.
Multiplicarea cu jucarii educationale
Cereți elevilor să creeze câte două seturi de câte cinci obiecte; arată rezultatul înmulțirii: 2 x 5 = 10. Apoi, să le rearanjăm obiectele în cinci grupe de câte două obiecte fiecare, demonstrând că 5 x 2 = 2 x 5. Pentru următoarea activitate, pentru a demonstra proprietatea asociativă, veți avea nevoie de 24 de obiecte sau de jucării educaționale. Împărțiți obiectele în jumătate și împărțiți fiecare jumătate în trei seturi de câte patru. Aratati ca jucariile reprezinta (3 x 4) x 2. Acum rearanjati obiectele in trei grupe, fiecare cu patru seturi de doua. Arătați că acest nou aranjament reprezintă 3 x (4 x 2). Provocați elevilor să sugereze modalități diferite de a obține același număr total de obiecte.